椭圆曲线加密简介

知道公钥加密算法的人应该已经听说过ECC\ECDH\ECDSA。 ECC是椭圆曲线加密算法(Elliptic Curve Cryptography)的缩写，其他两个是基于ECC的。
如今可以在现代web及IT领域基础的三个主要技术(TLS\PGP\SSH)中找到椭圆曲线加密算法的应用。更不用说加密货币(crypto currencies)了。
在ECC流行之前，几乎所有的公钥算法都是基于RSA，DSA和DH的，基于模运算的替代密码系统。RSA等加密算法直到今天依然很重要，经常和ECC并行使用。然而RSA的原理很容易解释和理解，粗略的实现也很容易写出来，但ECC的原理对于大多数人依然是个谜。

椭圆曲线(Elliptic Curves)

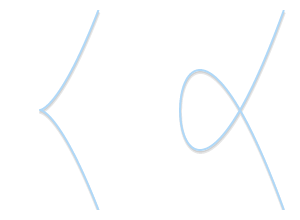首先，什么是椭圆(elliptic)曲线(curves)？Wolfram Mathworld给了一个完整定义，但就我们的目标而言，椭圆曲线是如下公式所描述的点的集合： $$ y^2 = x^3 + ax +b $$ $4a^3+27b^2\neq 0$是用来排除奇异(singular)曲线的，$y^2 = x^3 + ax +b$被称为椭圆曲线的Weierstrass范式（weierstrass normal form）。 下图是b=1,a=2 ... -3 时不同的椭圆曲线的不同形状 下图是奇点(singularities)类型：左侧是带尖的曲线（$y^2 = x^3$）。右侧是自相交的曲线($y^2 = x^3 - 3x +2$)。他们都不是有效的椭圆曲线。 依赖于a、b的值，椭圆曲线表现出不同的形状。显而易见，椭圆曲线是基于x轴(x-axis)对称(symmetric)的。
对于我们的目标，我们需要一个无穷远(Infinity)的点，也称为理想点(Ideal point)，成为我们的曲线的一部分。从现在起，我们用符号0代表(denote)这个理想点。
如果我们想明确地(explicitly)考虑(take into account)理想点，我们可以改进(refine)椭圆曲线的定义为下面的公式。 $$ \left{ (x, y) \in \mathbb{R}^2\ |\ y^2 = x^3 + ax + b,\ 4 a^3 + 27 b^2 \ne 0 \right}\ \cup\ \left{ 0 \right} $$

群(Groups)

数学中的群是一个被我们定义了加法(addition)的二元运算的集合，加法用符号+表示。
为了让集合$\mathbb{G}$成为群，加法必须遵守(respects)下面四个属性：

1. 封闭性(closure) 如果a和b都是$\mathbb{G}$的成员，那么a + b也必须是$\mathbb{G}$的成员；

2. 结合律(associativity) $$ (a+b) + c = a + (b+c) $$

3. 有单位元（幺元素 Identity element） 存在幺元素0，使得$a + 0 = 0 + a = a$

4. 有逆元 每个元素都有一个inverse，使得每个a都存在b，$a+ b = 0$. 如果我们添加第五个要求：

5. 交换律(commutativity) $$ a + b = b + a $$ 那么这个群被称为阿贝尔群(abelian group)

在通常的加法的概念中，整数集合$\mathbb{Z}$是一个群，而且是阿贝尔群。而自然数集合$\mathbb{N}$不是群，因为他没有逆元。
如果我们能证明前四个属性（封闭性、结合律、有单位元和逆元）成立，就能得到其他的属性。
例如：幺元素是唯一的；逆元也是唯一的。对于每个a，都有且只有一个b使得$ a+b =0$，b也可以写做-a。群的属性对我们之后的使用都有直接间接的重要作用。

椭圆曲线的群法则

我们可以定义一个椭圆曲线上的群，约定：

• 群中的元素都是椭圆曲线上的点；
• 幺元素是无穷0上的点；
• P点及其逆元关于X轴对称；
• 加法遵守这个规则：给定三个对齐的非零点 P、Q、R，他们的和等0（$P+Q+R=0$）。 注意最后一点，我们只要求3个点是对齐的，没要求他们的顺序。也就是说，如果P、Q、R对齐了，那么$P+(Q+R)=Q+(P+R)=R+(P+Q)= ... = 0$.
  以这种方式，我们直观地(intuitively)证明了我们的加法操作既遵守了结合律也遵守了交换律，这就是一个阿贝尔群了。

几何意义的加法(Geometric addition)

得益于我们现在就在使用一个阿贝尔群，我们可以把$P+Q+R=0$写成$P+Q=-R$。
这个公式形式让我们得到(derive)一个计算点P与点Q的和的几何方法。
如果我们画一条通过点P和点Q的直线，这条线会与曲线相交(intersect)于第三点R。如果我们取点R的逆元-R，我们就得到了P+Q的结果。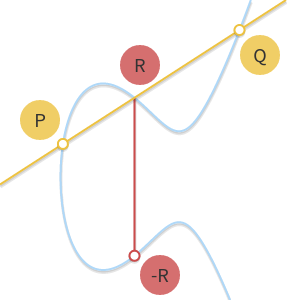

这个几何方法有效，但是需要改进(refinement)。尤其是面对下面的情况：

• $P=0$或 $Q=0$ 0不在xy坐标系上，画不出这样的线。但是考虑到(given that)我们已经把0定义为幺元素，对于任何P和任何Q都有$P+0=P$和$0+Q=Q$。
• $P=-Q$ 直线垂直通过椭圆的两个点，不与第三点相交。但如果P是Q的逆元，从逆元的定义中可知$P+Q=P+(-P)=0$
• $P=Q$ 这时会有无穷多的线会穿过点，情况就变得复杂了。但如果$Q' \neq P$，Q'无限接近P时会发生什么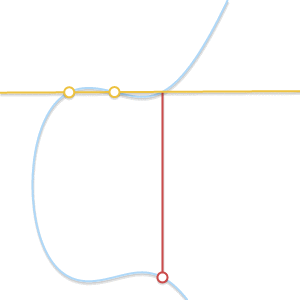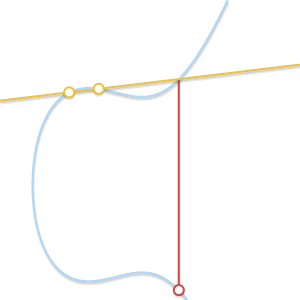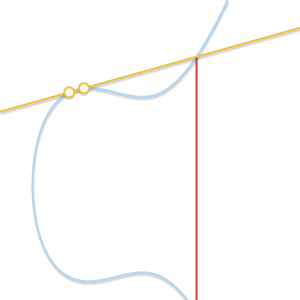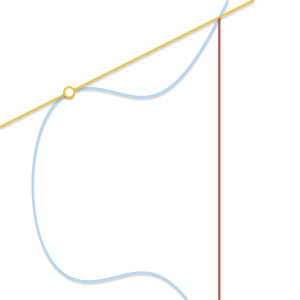？ 随着Q'趋近P，穿过两点的线变成椭圆的切线。根据(in the light of)这个现象，我们可以说$P+P=-R$，点R就是曲线和过点P的切线的交点。
• $P \neq Q$，但是没有第三个点R 与$P=Q$的情况很相似。事实上，这种情况就是经过同时经过P和Q的椭圆切线。 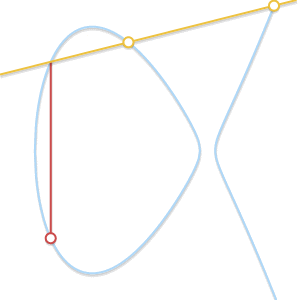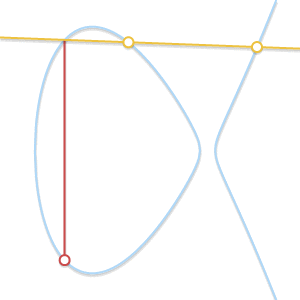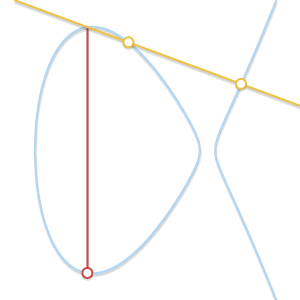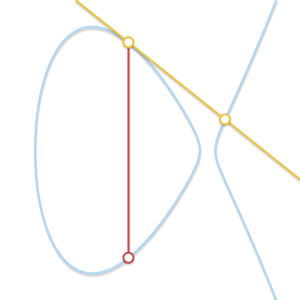把点P视为切点，上面的情况我们可以写成$P+P=-Q$。这个公式就成了$P+Q=-P$。反过来，Q视为切点，公式就变成了$P + Q = -Q$。
  几何方法现在已经完整覆盖了所有情况。用尺和笔就能计算任意椭圆曲线上任意点的加法了。

代数意义的加法(Algebraic addition)

如果我们想让计算机执行椭圆曲线上的加法，我们就需要把几何方法转换为代数方法。
把上面的方法转换成一系列方程可能看起来并不复杂（straightforward），但实际上这个过程很繁琐(tedious)，因为他需要解(solving)立方(cubic)方程。所以这里只写结果。
首先，摆脱(get rid of)最烦人(annoying)的边边角角(corner)的情况。已知$P + (-P)=0$，也已知$P+0=0+P=P$。所以在我们的方程中要避免这两种情况，只考虑P和Q都非0且不对称的情况。$P=(x_P, y_P)$ $Q=(x_Q,y_Q)$
如果P和Q是不同的(distinct)，$x_P \neq x_Q$，直线的斜率(slope)方程如下 $$ m = \frac{y_P - y_Q}{x_P - x_Q} $$ 直线与椭圆曲线的交点$R=(x_R,y_r)$: $$ x_R = m^2 - x_P - x_Q \ y_R = y_P + m(x_R - x_P) $$ 或者 $$ y_R=y_Q+m(x_R-x_Q) $$ 因为$(x_P,y_P) + (x_Q,y_Q) = (x_R,-y_R)$，注意符号，并且记住$P+Q=-R$。
如果我们想检查结果是否正确，我们就不得不检查点R是否在曲线上，并且点P、Q、R是否对齐。
检查三点是否对齐相对简单，但检查R是否在曲线上就不是了，因为需要做立方计算。
举个例子：
给定$P=(1,2)$和$Q=(3,4)$，曲线方程为$y^2=x^3-7x+10$，计算的和为$P+Q=-R=(-3,2)$。
验证过程： $$ m &= \frac{y_P - y_Q}{x_P - x_Q} = \frac{2 - 4}{1 - 3} = 1 \ x_R &= m^2 - x_P - x_Q = 1^2 - 1 - 3 = -3 \ y_R &= y_P + m(x_R - x_P) = 2 + 1 \cdot (-3 - 1) = -2 \ &= y_Q + m(x_R - x_Q) = 4 + 1 \cdot (-3 - 3) = -2 $$ 结果是正确的。
即使P或Q是切点也是有效的。假设$P=(-1,4)$并且$Q=(1,2)$。 $$ m & = \frac{y_P - y_Q}{x_P - x_Q} = \frac{4 - 2}{-1 - 1} = -1 \ x_R & = m^2 - x_P - x_Q = (-1)^2 - (-1) - 1 = 1 \ y_R & = y_P + m(x_R - x_P) = 4 + -1 \cdot (1 - (-1)) = 2 $$

当$P=Q$时，有一些不同。$x_R$和$y_R$的计算方程和之前是一样的，但是斜率方程要修改： $$ m = \frac{3 x_P^2 + a}{2 y_P} $$

标量乘法(Scalar multiplication)

除了加法之外，我们可以定义另一个操作——标量乘法： $$ nP = \underbrace{P + P + \cdots + P}_{n\ \text{times}} $$ 其中n是自然数。
写成这种格式，可以将计算nP看作n次加法。如果n转换成二进制后长度为k，那么我们的算法的复杂度会变成$O(2^k)$，非常的不优雅。但是还有更快的算法。
其中一种算法就是倍加算法(double and add)。它的操作原理用下面的例子会很好解释。设$n=151$，二进制表示为$10010111_2$。这个二进制表示可以被转换为两个幂运算的和。 $$ 151 & = 1 \cdot 2^7 + 0 \cdot 2^6 + 0 \cdot 2^5 + 1 \cdot 2^4 + 0 \cdot 2^3 + 1 \cdot 2^2 + 1 \cdot 2^1 + 1 \cdot 2^0 \ & = 2^7 + 2^4 + 2^2 + 2^1 + 2^0 $$ 上面的操作就是把n的每个二进制位与2的幂运算相乘。
然后可以写成：
$$ 151 \cdot P = 2^7 P + 2^4 P + 2^2 P + 2^1 P + 2^0 P $$ 最后，我们通过7次倍乘和4次加法得到了结果。
用python代码实现是这样的：

def bits(n):
    """
    Generates the binary digits of n, starting
    from the least significant bit.

    bits(151) -> 1, 1, 1, 0, 1, 0, 0, 1
    """
    while n:
        yield n & 1
        n >>= 1

def double_and_add(n, x):
    """
    Returns the result of n * x, computed using
    the double and add algorithm.
    """
    result = 0
    addend = x

    for bit in bits(n):
        if bit == 1:
            result += addend
        addend *= 2

    return result

对数(Logarithm)

:::warn 这一大段没有看明白，所以几乎没翻译。 感觉上是想说正常运算$Q=nP$比较简单，但想逆运算求出n需要解决对数难题，类似于逆向RSA的感觉，以此来证明椭圆曲线在加密场景下的安全性。 ::: 给定n和P，我们现在至少有一个计算$Q=nP$的多项式时间算法(polynomial-time algorithm)。但如果反过来已知Q和P需要求n呢？这个问题就是对数问题(logarithm problem)。我们称它为对数而不是除法(division)以遵守(conformity)其他加密系统的要求。

个人理解

上面给出的方程都比较好计算，主要是阿贝尔群的加法和平时的加法不大一样，所以有一点理解上的门槛。
因为椭圆曲线经过了三次幂的计算，所以逆向计算时更麻烦，感觉上和RSA的超大实数幂运算不相上下。

引用

Elliptic Curve Cryptography: a gentle introduction